Data-driven Process Systems Engineering Lab
Publications
Surrogate-based branch-and-bound algorithms for simulation-based black-box optimization
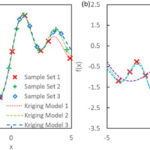
Optimization and Engineering 2022
Black-box surrogate-based optimization has received increasing attention due to the growing interest in solving optimization problems with embedded simulation data. The main challenge in surrogate-based optimization is the lack of consistently convergent behavior, due to the variability introduced by initialization,…
Data-Driven Simultaneous Process Optimization and Adsorbent Selection for Vacuum Pressure Swing Adsorption
Chemical Engineering Research and Design 2022
Technologies for post-combustion carbon capture are essential for the reduction of greenhouse gas emissions to the atmosphere. However, they are still associated with high costs and energy consumption. Intensified processes for carbon capture have the potential to overcome these challenges…
Stages and Kinetics of Mechanochemical Depolymerization of Poly(ethylene terephthalate) with Sodium Hydroxide
ACS Sustainable Chem. Eng. 2022
Efficient chemical recycling of consumer plastics (i.e., depolymerization down to monomers) is a crucial step needed to achieve a circular material economy. In this work, depolymerization of poly(ethylene terephthalate) (PET) via mechanochemical hydrolysis with sodium hydroxide is studied, with complete…
Perspectives on the Integration between First-Principles and Data-Driven Modeling
Computers & Chemical Engineering 2022
Efficiently embedding and/or integrating mechanistic information with data-driven models is essential if it is desired to simultaneously take advantage of both engineering principles and data-science. The opportunity for hybridization occurs in many scenarios, such as the development of a faster…
Two-Stage Approach to Parameter Estimation of Differential Equations Using Neural ODEs
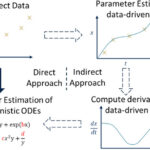
Industrial & Engineering Chemistry Research 2021
Modeling physiochemical relationships using dynamic data is a common task in fields throughout science and engineering. A common step in developing generalizable, mechanistic models is to fit unmeasured parameters to measured data. However, fitting differential equation-based models can be computation-intensive…
AC-Optimal Power Flow Solutions with Security Constraints from Deep Neural Network Models
Computer Aided Chemical Engineering 2021
In power grid operation, optimal power flow (OPF) problems are solved several times per day to find economically optimal generator setpoints that balance given load demands. Ideally, we seek an optimal solution that is also “N-1 secure”, meaning the system can…
Data-driven Spatial Branch-and-bound Algorithm for Box-constrained Simulation-based Optimization
Journal of Global Optimization 2021
The ability to use complex computer simulations in quantitative analysis and decision-making is highly desired in science and engineering, at the same rate as computation capabilities and first-principle knowledge advance. Due to the complexity of simulation models, direct embedding of…
Surrogate-Based Optimization for Mixed-Integer Nonlinear Problems
Computers & Chemical Engineering 2020
Simulation-based optimization using surrogate models enables decision-making through the exchange of data from high-fidelity models and development of approximations. Many chemical engineering optimization problems, such as process design and synthesis, rely on simulations and contain both discrete and continuous decision…
Managing Uncertainty in Data-Driven Simulation-Based Optimization
Computers & Chemical Engineering 2019
Optimization using data from complex simulations has become an attractive decision-making option, due to ability to embed high-fidelity, non-linear understanding of processes within the search for optimal values. Due to lack of tractable algebraic equations, the link between simulations and…
Machine learning-based surrogate modeling for data-driven optimization: a comparison of subset selection for regression techniques
Optimization Letters 2019
Optimization of simulation-based or data-driven systems is a challenging task, which has attracted significant attention in the recent literature. A very efficient approach for optimizing systems without analytical expressions is through fitting surrogate models. Due to their increased flexibility, nonlinear…
