Two-Stage Approach to Parameter Estimation of Differential Equations Using Neural ODEs

Industrial & Engineering Chemistry Research 2021

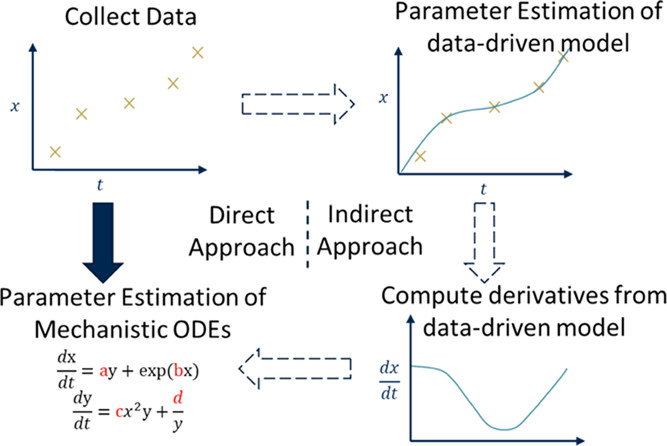
Modeling physiochemical relationships using dynamic data is a common task in fields throughout science and engineering. A common step in developing generalizable, mechanistic models is to fit unmeasured parameters to measured data. However, fitting differential equation-based models can be computation-intensive and uncertain due to the presence of nonlinearity, noise, and sparsity in the data, which in turn causes convergence to local minima and divergence issues. This work proposes a merger of machine learning (ML) and mechanistic approaches by employing ML models as a means to fit nonlinear mechanistic ordinary differential equations (ODEs). Using a two-stage indirect approach, neural ODEs are used to estimate state derivatives, which are then used to estimate the parameters of a more interpretable mechanistic ODE model. In addition to its computational efficiency, the proposed method demonstrates the ability of neural ODEs to better estimate derivative information than interpolating methods based on algebraic data-driven models. Most notably, the proposed method is shown to yield accurate predictions even when little information is known about the parameters of the ODEs. The proposed parameter estimation approach is believed to be most advantageous when the ODE to be fit is strongly nonlinear with respect to its unknown parameters.

Link to Publication