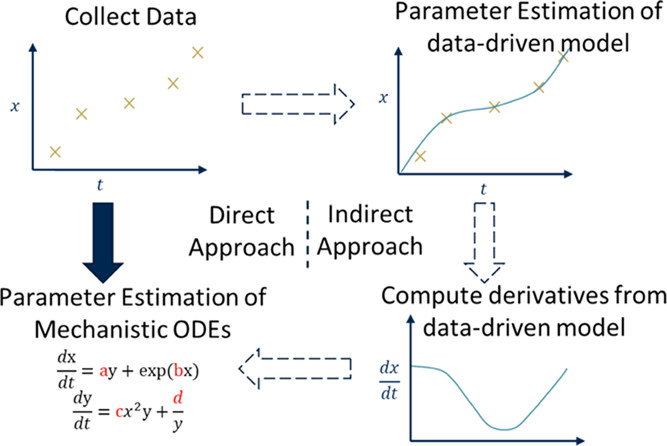
A common step in developing generalizable, dynamic mechanistic models is to fit unmeasured parameters to measured data. Fitting differential equation-based models can be computationally expensive due to the presence of nonlinearity and stiffness. This work proposes a two-stage indirect approach where Neural ODEs approximate state derivatives, which are used to estimate the parameters of a differential model. In addition to its computational efficiency, the proposed method demonstrates the ability to work in concert with direct methods to accurately estimate parameters, even in the case of stiff systems. The method is shown here for the training of a microkinetic model.