Surrogate-Based Optimization for Mixed-Integer Nonlinear Problems

Computers & Chemical Engineering 2020

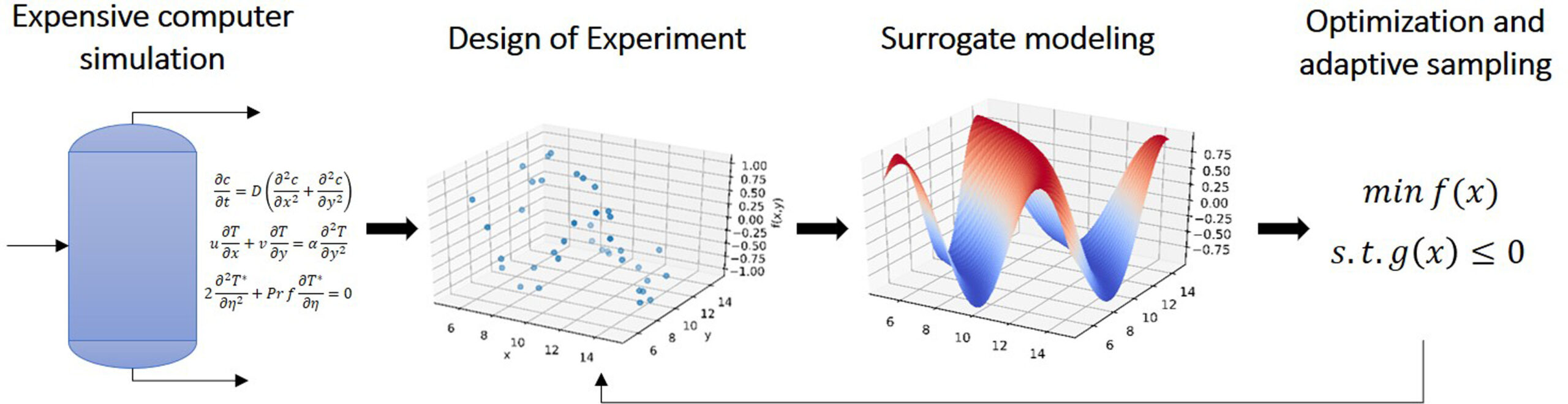
Simulation-based optimization using surrogate models enables decision-making through the exchange of data from high-fidelity models and development of approximations. Many chemical engineering optimization problems, such as process design and synthesis, rely on simulations and contain both discrete and continuous decision variables. Surrogate-based optimization with continuous variables has been studied extensively; however, there are many open challenges for the case of mixed-variable inputs. In this work, we propose an algorithm for mixed-integer nonlinear simulation-based problems that uses adaptive sampling and surrogate modeling with one-hot encoding. We propose techniques for the design of experiments for mixed-variable problems, surrogate modeling for mixed-variable response surfaces, and iterative approximation-optimization procedure that leads to optimal solutions. Results show that one-hot encoding leads to accurate and robust mixed-variable Gaussian Process and Neural Network models that are effective surrogates for optimization. The proposed algorithm is tested on mixed-integer nonlinear benchmark problems and a chemical process synthesis case study.

Link to Publication