Reduced order Discrete Element Method (DEM) modeling

Chemical Engineering Science 2013

F. Boukouvala F.J. Muzzio M.G. Ierapetritou Y. Gao

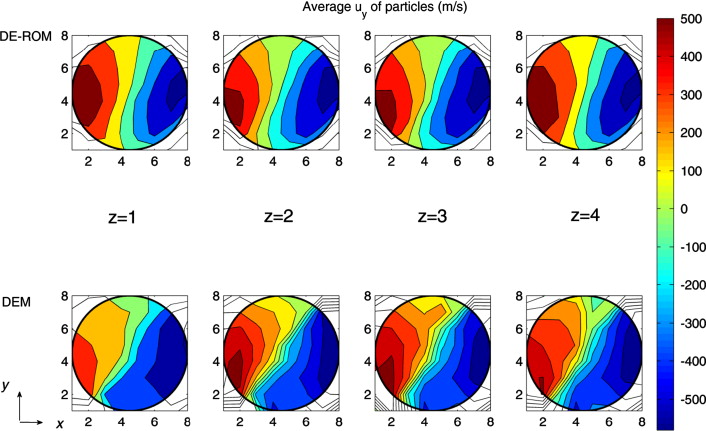
Reduced-order modeling (ROM) techniques are playing a very significant role in the recent literature bridging the gap between computationally expensive simulators and their application in optimization and control of distributed parameter systems. In modeling of solid-based processes, Discrete Element Method (DEM) is a very popular high-fidelity modeling approach which enables the tracking of discrete entities as they are processed inside complex geometries interacting with each other and with process boundaries. However, the computational cost of DEM models limits their applicability to simulation of specific and limited number of cases. In this work, we develop the DE–ROM (Discrete Element–Reducer-order model) approach which reduces the computational cost—while maintaining model accuracy—of expensive DEM models. The proposed methodology is based on Principal Component Analysis (PCA), combined with surrogate-model mapping and data imputation for the cases where there is missing information. The results of the application of the developed method to the powder mixing process, demonstrate that the DE–ROM model produces accurate profiles of distributed particle properties in real time. Finally, the developed model is used for the identification of the optimal design and operating conditions of the mixing process.

Link to Publication