Machine learning-based surrogate modeling for data-driven optimization: a comparison of subset selection for regression techniques

Optimization Letters 2019

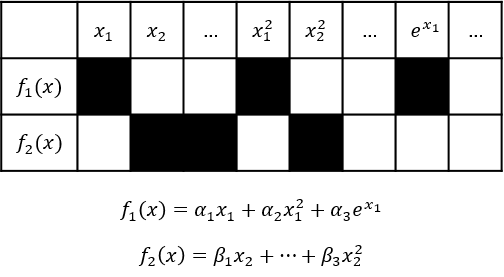
Optimization of simulation-based or data-driven systems is a challenging task, which has attracted significant attention in the recent literature. A very efficient approach for optimizing systems without analytical expressions is through fitting surrogate models. Due to their increased flexibility, nonlinear interpolating functions, such as radial basis functions and Kriging, have been predominantly used as surrogates for data-driven optimization; however, these methods lead to complex nonconvex formulations. Alternatively, commonly used regression-based surrogates lead to simpler formulations, but they are less flexible and inaccurate if the form is not known a priori. In this work, we investigate the efficiency of subset selection regression techniques for developing surrogate functions that balance both accuracy and complexity. Subset selection creates sparse regression models by selecting only a subset of original features, which are linearly combined to generate a diverse set of surrogate models. Five different subset selection techniques are compared with commonly used nonlinear interpolating surrogate functions with respect to optimization solution accuracy, computation time, sampling requirements, and model sparsity. Our results indicate that subset selection-based regression functions exhibit promising performance when the dimensionality is low, while interpolation performs better for higher dimensional problems.

Link to Publication