Derivative-free optimization for expensive constrained problems using a novel expected improvement objective function

AIChE Journal 2014

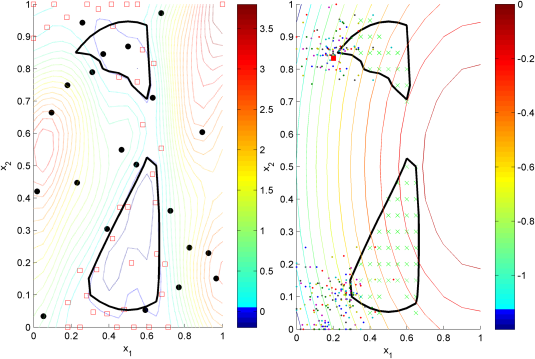
In this work, an algorithm for the optimization of costly constrained systems is introduced. The proposed method combines advantages of global- and local-search algorithms with new concepts of feasibility space mapping, within a framework that aims to find global solutions with minimum sampling. A global search is initially performed, during which kriging surrogate models of the objective and the feasible region are developed. A novel search criterion for locating feasibility boundaries is introduced, which does not require any assumptions regarding the convexity and nonlinearity of the feasible space. Finally, local search is performed starting from multiple locations identified by clustering of previously obtained samples. The performance of the proposed approach is evaluated through both benchmark examples and a case study from the pharmaceutical industry. A comparison of the method with commercially available software reveals that the proposed method has a competitive performance in terms of sampling requirements and quality of solution

Link to Publication