Nonlinear Variable Selection Algorithms for Surrogate Modeling

AIChE Journal 2019

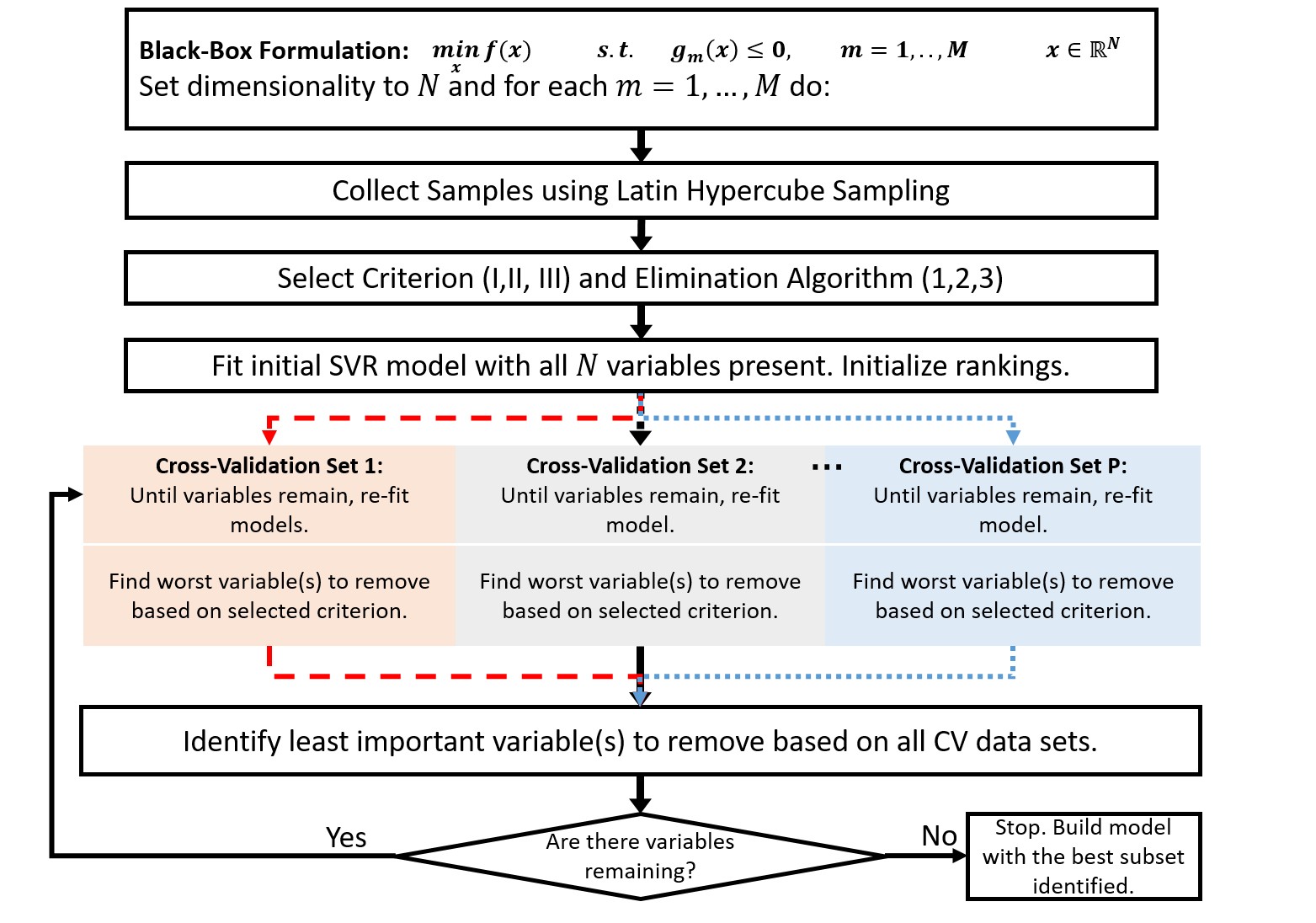
Having the ability to analyze, simulate and optimize complex systems is becoming more important in all engineering disciplines. Decision-making using complex systems usually leads to nonlinear optimization problems, which rely on computationally expensive simulations. Therefore, it is often challenging to detect the actual structure of the optimization problem and formulate these problems with closed-form analytical expressions. Surrogate-based optimization of complex systems is a promising approach based on the concept of adaptively fitting and optimizing approximations of the input-output data. Standard surrogate-based optimization assumes the degrees of freedom are known a-priori; however, in real applications the sparsity and the actual structure of the black-box formulation may not be known. In this work, we propose to select the correct variables contributing to each objective function and constraints of the black-box problem, by formulating the identification of the true sparsity of the formulation as a non-linear feature selection problem. We compare three variable selection criteria based on Support Vector Regression and develop efficient algorithms to detect the sparsity of black-box formulations when only a limited amount of deterministic or noisy data is available.

Link to Publication